What Are Split Scores?

(This is the 10th post in a series that started here)

Up until now, I’ve been talking a lot about the rate of change for marathon splits and not as much about the raw splits themselves.

That’s because raw split numbers aren’t always a very good way to compare splits, especially between individual runners.

Think about it. If a runner runs a 1:30 first half of a marathon and a 1:40 second half, she’s run a 3:10 marathon with a 10-minute positive split. Simple, right?

Now, suppose another runner runs a 2:30 first half and a 2:40 second half. That’s a 5:10 marathon, also with a 10-minute positive split.

Ten minutes is ten minutes. So when we compare the two races, both runners ran the same positive split, right?

Not really. 10 minutes is proportionally larger when compared to a 3:10 marathon than it is when compared to a 5:10. Just because both of them had raw splits of 10 minutes, saying that the splits are the same isn’t right. The 5:10 runner clearly ran closer to even splits than the 3:10 runner.

So if we’re going to look at runners and compare their splits or add splits together to analyze them in groups, we need to come up with a better way of assigning a value to each set of splits, a “spilt score” if you will.

It doesn’t have to be complicated. Let’s define a “split score” as “how far a runner is from even splits, relative to their finish time”.

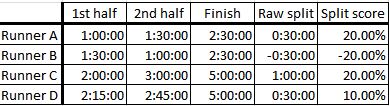
Here are some sample splits:

Click any image to enlarge

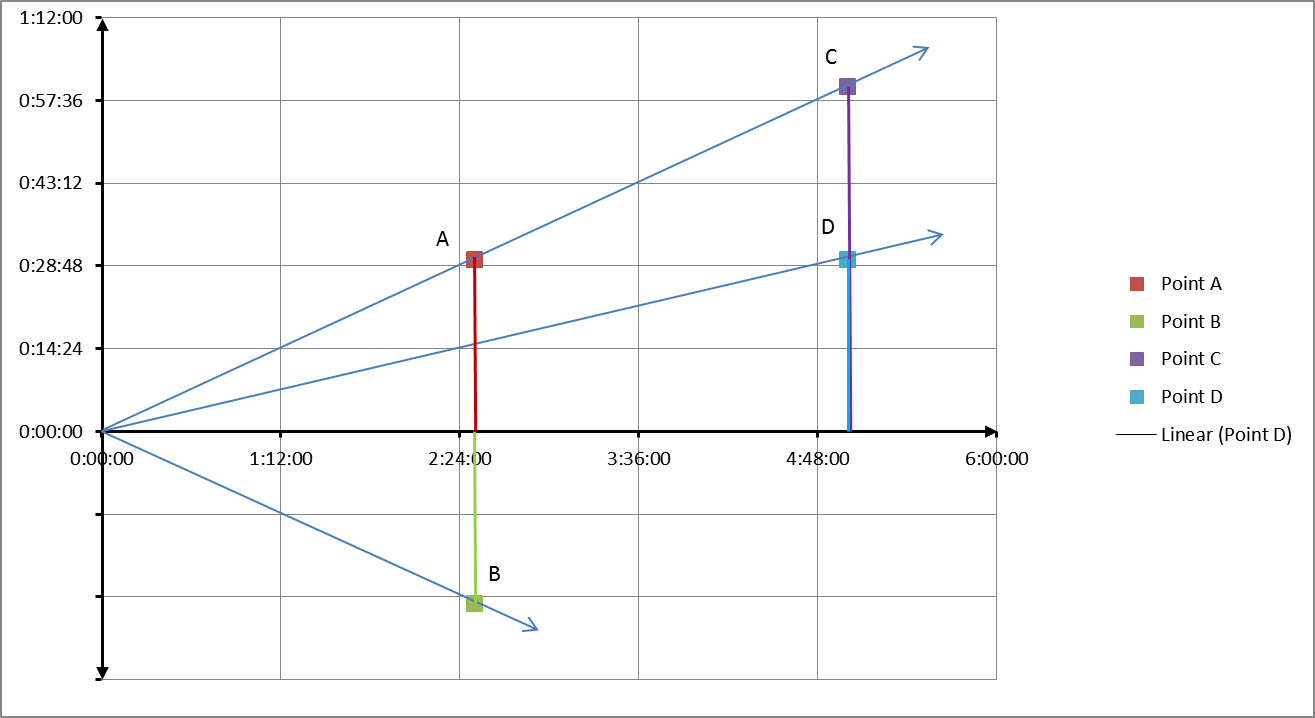
I’ve plotted them on this chart:

Runner A ran a 2:30 by running a 1:00 first half (wow!) and a 1:30 second half, giving him a raw split of 30 minutes (represented by the red line).

Our initial “split score” for A is 30 minutes divided by 2 hours and 30 minutes, or .2.

Note that the result is just “.2”, not “.2 minutes”. Since we’re dividing a time by a time, the “time” part drops out, leaving us with what they call a “dimensionless number”.

Most of us don’t have an intuitive feel for what a split of “point 2” means. To convert the score to something we do understand, we can turn it into a percentage by multiplying by 100. So A ends up with a split score of 20%.

Both runner C and runner D took 5 hours to finish the race, twice as long as runner A. Runner C’s raw split is 1 hour, also twice runner A’s, so C’s split score is also 20%.

On the other hand, while runner D’s raw split of 30 minutes is equal to runner A’s, since D’s finish time is twice A’s, D’s split score is half of A’s, or 10%.

Of course, as runner B shows, split scores can be negative, too (a 1:00 second half!?!).

We’ll start to find out what, if anything, split scores are good for in my next post.